Data Analytics and Visualization using R

In this document we used R to do the automate data analytics using R programming language, an open-source language used for statistical computing and graphics

Source: Human-Capital

Hypothesis

  • H0: There is no significant difference between the Information officers and Industrial workers

  • H1: There is significant difference between the Information officers and Industrial workers

  • H0: The salary/wage has no significant influence on education, race, and job-class

  • H1: The salary/wage has significant influence on education, race, and job-class

Below are the variables we are going to used for this Data Analysis

Table2 Demographic Characteristics

Characteristic N = 3,0001
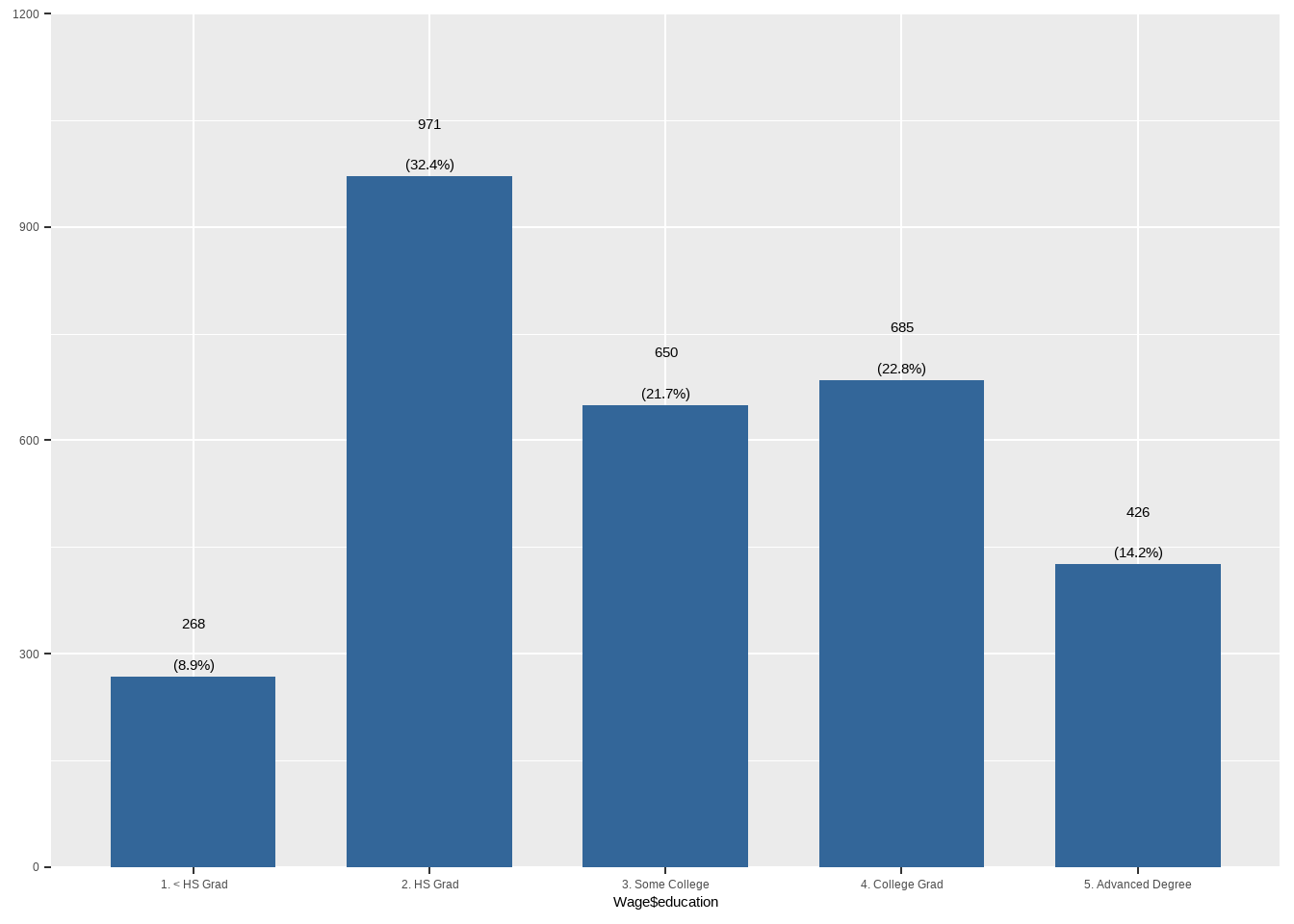
education
    1. < HS Grad 268 (8.9%)
    2. HS Grad 971 (32%)
    3. Some College 650 (22%)
    4. College Grad 685 (23%)
    5. Advanced Degree 426 (14%)
age 42 (34, 51)
health
    1. <=Good 858 (29%)
    2. >=Very Good 2,142 (71%)
1 n (%); Median (IQR)

Table2 Distribution by Marital Status

Characteristic N = 3,0001
maritl
    1. Never Married 648 (22%)
    2. Married 2,074 (69%)
    3. Widowed 19 (0.6%)
    4. Divorced 204 (6.8%)
    5. Separated 55 (1.8%)
health_ins
    1. Yes 2,083 (69%)
    2. No 917 (31%)
1 n (%)

Table2 Socio-economic factors

Characteristic N = 3,0001
wage 105 (85, 129)
jobclass
    1. Industrial 1,544 (51%)
    2. Information 1,456 (49%)
race
    1. White 2,480 (83%)
    2. Black 293 (9.8%)
    3. Asian 190 (6.3%)
    4. Other 37 (1.2%)
1 Median (IQR); n (%)
Characteristic N = 3,0001
region
    1. New England 0 (0%)
    2. Middle Atlantic 3,000 (100%)
    3. East North Central 0 (0%)
    4. West North Central 0 (0%)
    5. South Atlantic 0 (0%)
    6. East South Central 0 (0%)
    7. West South Central 0 (0%)
    8. Mountain 0 (0%)
    9. Pacific 0 (0%)
1 n (%)
Characteristic N = 3,0001
year
    2003 513 (17%)
    2004 485 (16%)
    2005 447 (15%)
    2006 392 (13%)
    2007 386 (13%)
    2008 388 (13%)
    2009 389 (13%)
1 n (%)

Linear regression analysis

Parameter                 | Coefficient |           95% CI | t(2998) |      p | Std. Coef. | Std. Coef. 95% CI |      Fit
-------------------------------------------------------------------------------------------------------------------------
(Intercept)               |      103.32 | [101.28, 105.36] |   99.43 | < .001 |      -0.20 |    [-0.25, -0.15] |         
jobclass [2. Information] |       17.27 | [ 14.35,  20.20] |   11.58 | < .001 |       0.41 |    [ 0.34,  0.48] |         
                          |             |                  |         |        |            |                   |         
AIC                       |             |                  |         |        |            |                   | 30774.50
AICc                      |             |                  |         |        |            |                   | 30774.51
BIC                       |             |                  |         |        |            |                   | 30792.52
R2                        |             |                  |         |        |            |                   |     0.04
R2 (adj.)                 |             |                  |         |        |            |                   |     0.04
Sigma                     |             |                  |         |        |            |                   |    40.83

In this section we used a report function to generate the narrative of binary linear regression

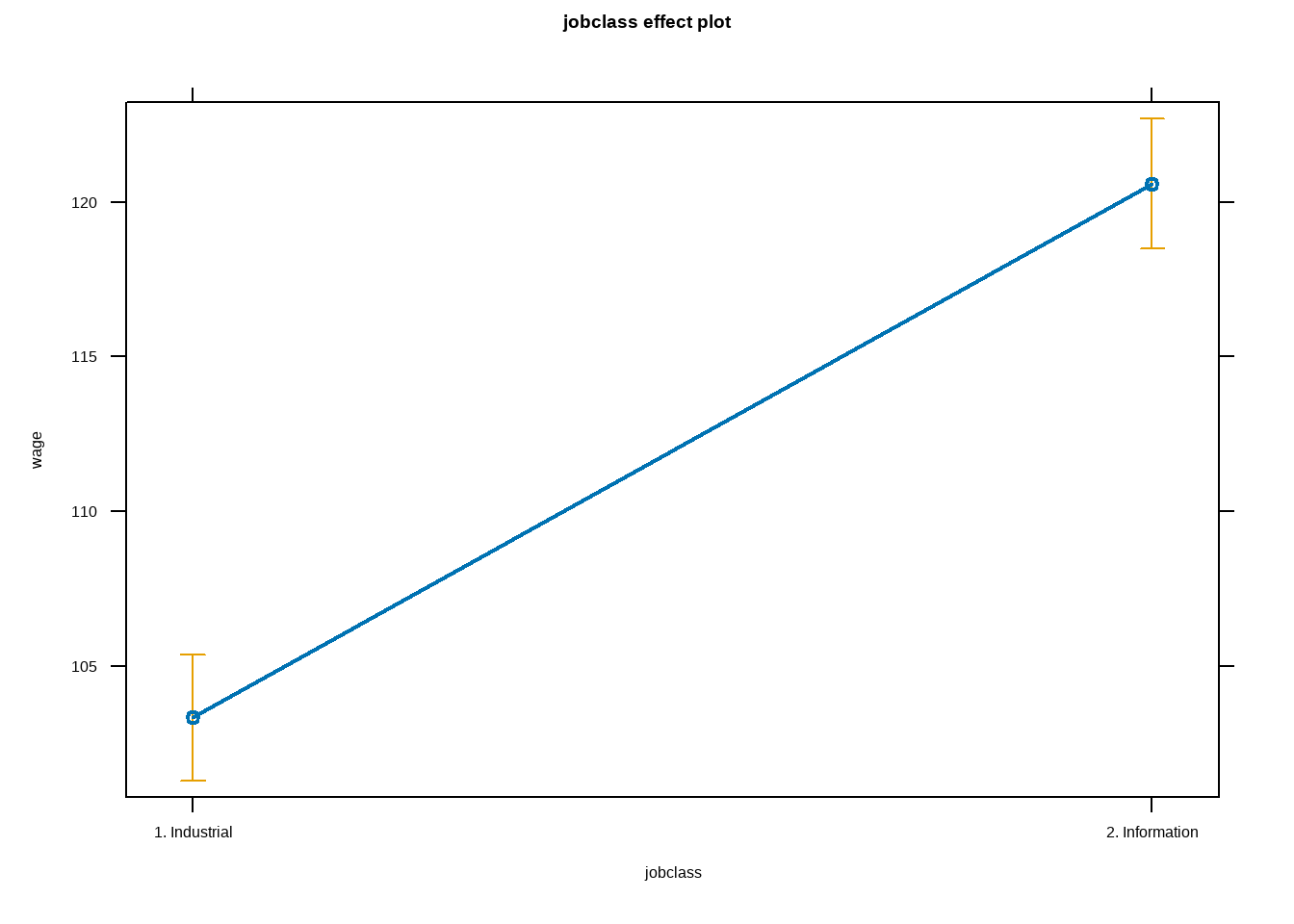
We fitted a linear model (estimated using OLS) to predict wage with jobclass (formula: wage ~ jobclass). The model explains a statistically significant and weak proportion of variance (R2 = 0.04, F(1, 2998) = 134.07, p < .001, adj. R2 = 0.04). The model’s intercept, corresponding to jobclass = 1. Industrial, is at 103.32 (95% CI [101.28, 105.36], t(2998) = 99.43, p < .001). Within this model:

  • The effect of jobclass [2. Information] is statistically significant and positive (beta = 17.27, 95% CI [14.35, 20.20], t(2998) = 11.58, p < .001; Std. beta = 0.41, 95% CI [0.34, 0.48])

Standardized parameters were obtained by fitting the model on a standardized version of the dataset. 95% Confidence Intervals (CIs) and p-values were computed using a Wald t-distribution approximation.

Multiple linear regression

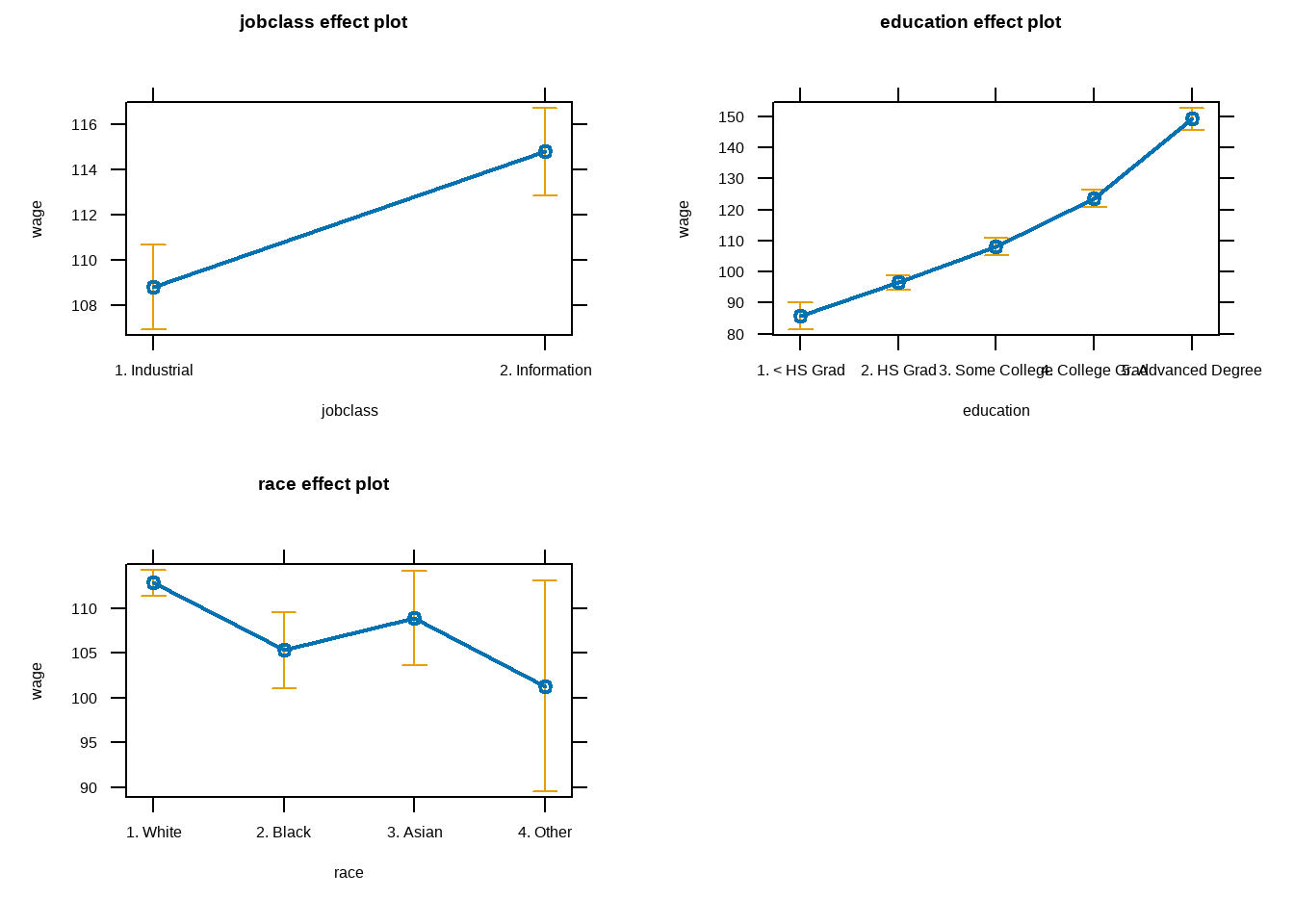
analysis in this model we are going to explore the influence of wage/salary as dependent variables and Age, Race, Education, and Marital status of the employee

Table of multiple logistics regression analysis

Characteristic Beta 95% CI1 p-value
jobclass


    1. Industrial — —
    2. Information 6.0 3.2, 8.8 <0.001
education


    1. < HS Grad — —
    2. HS Grad 11 5.9, 16 <0.001
    3. Some College 22 17, 28 <0.001
    4. College Grad 38 33, 43 <0.001
    5. Advanced Degree 63 58, 69 <0.001
race


    1. White — —
    2. Black -7.5 -12, -3.1 <0.001
    3. Asian -4.0 -9.4, 1.5 0.2
    4. Other -12 -23, 0.33 0.057
1 CI = Confidence Interval

Model Explanation

ExpCatViz( 
  Wage %>% 
    select(education, jobclass),
  target = "education"
  )
[[1]]

plot_frq(Wage$education)

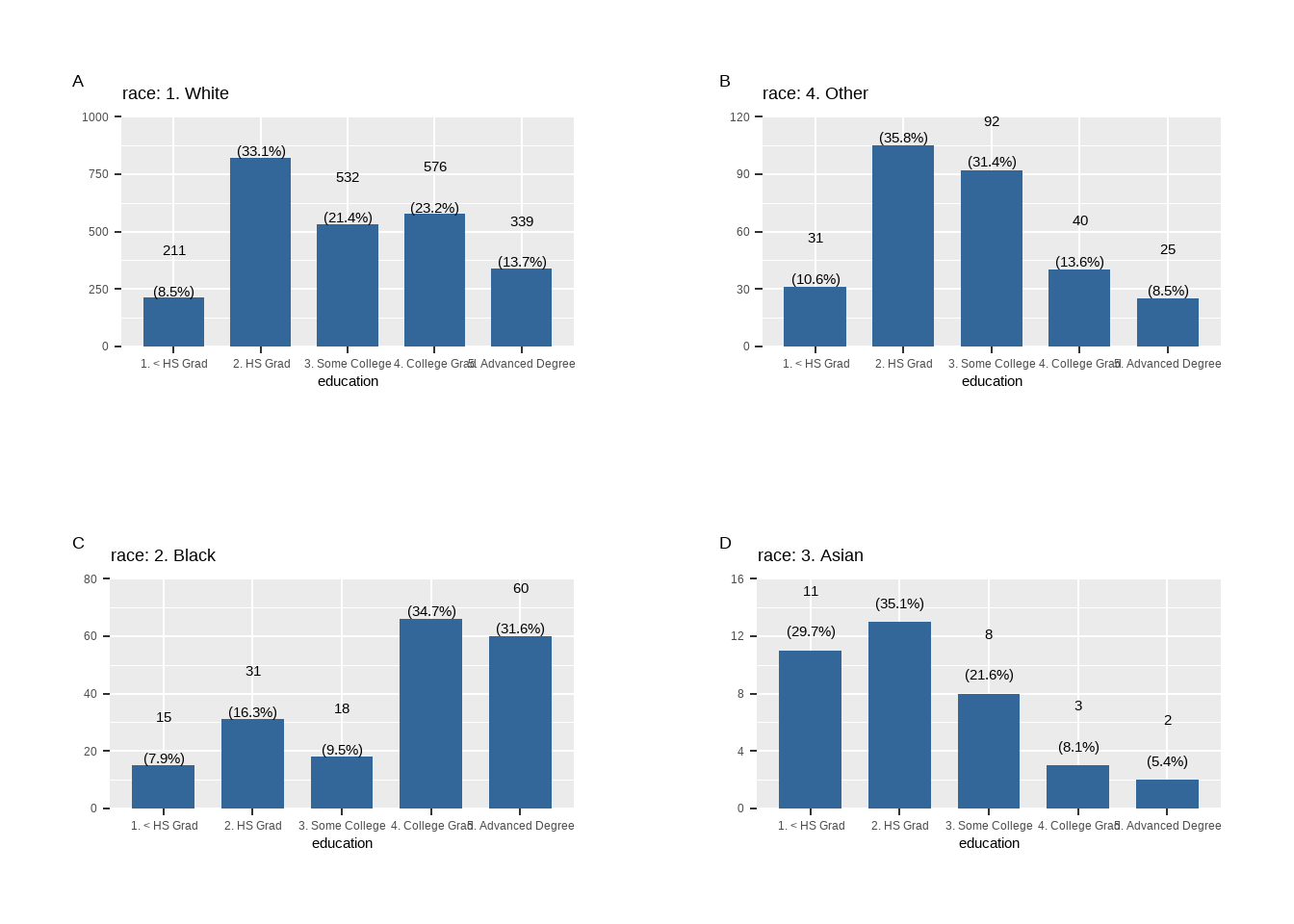
Wage %>% 
  group_by(race) %>% 
  plot_frq(education) %>% 
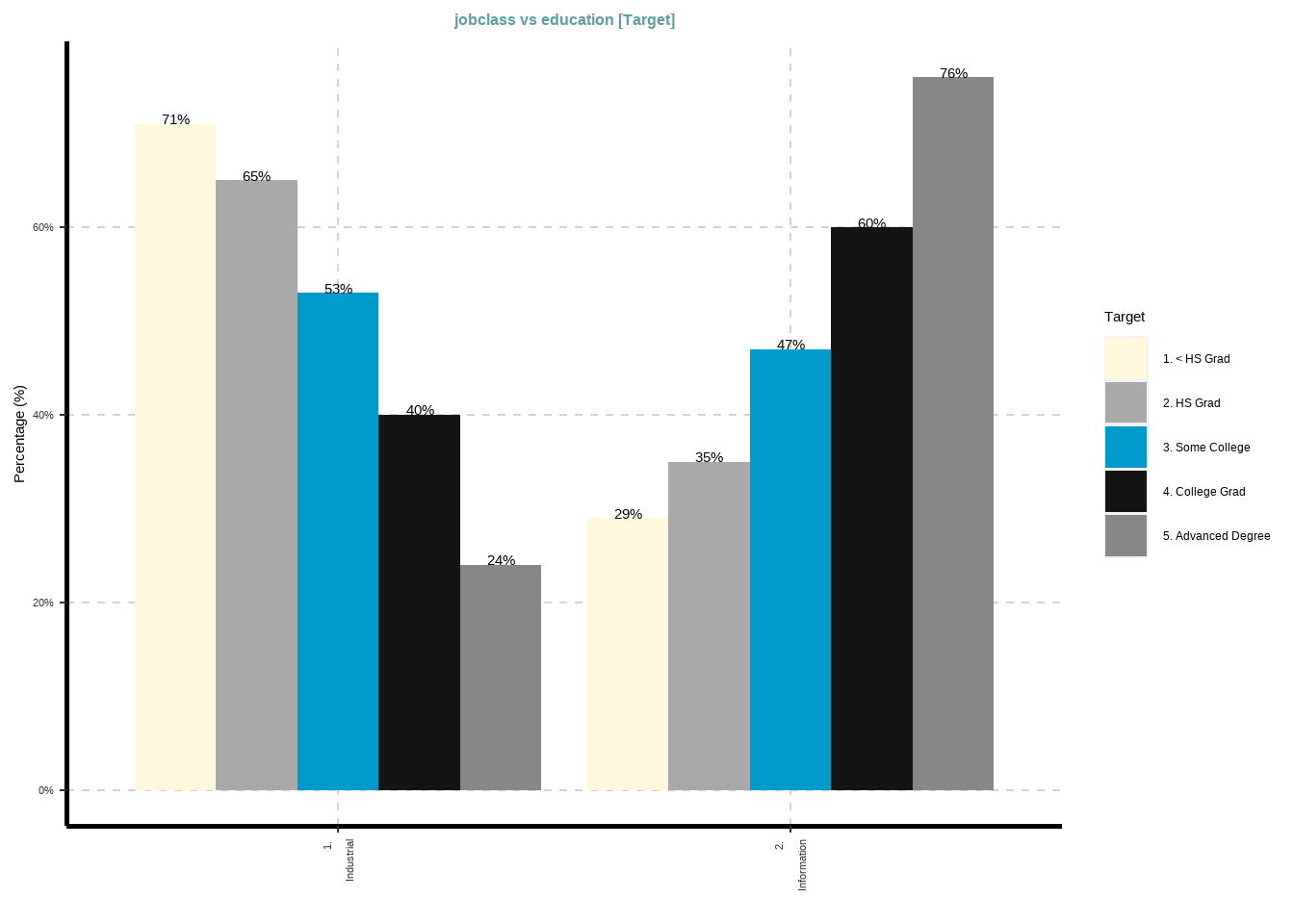
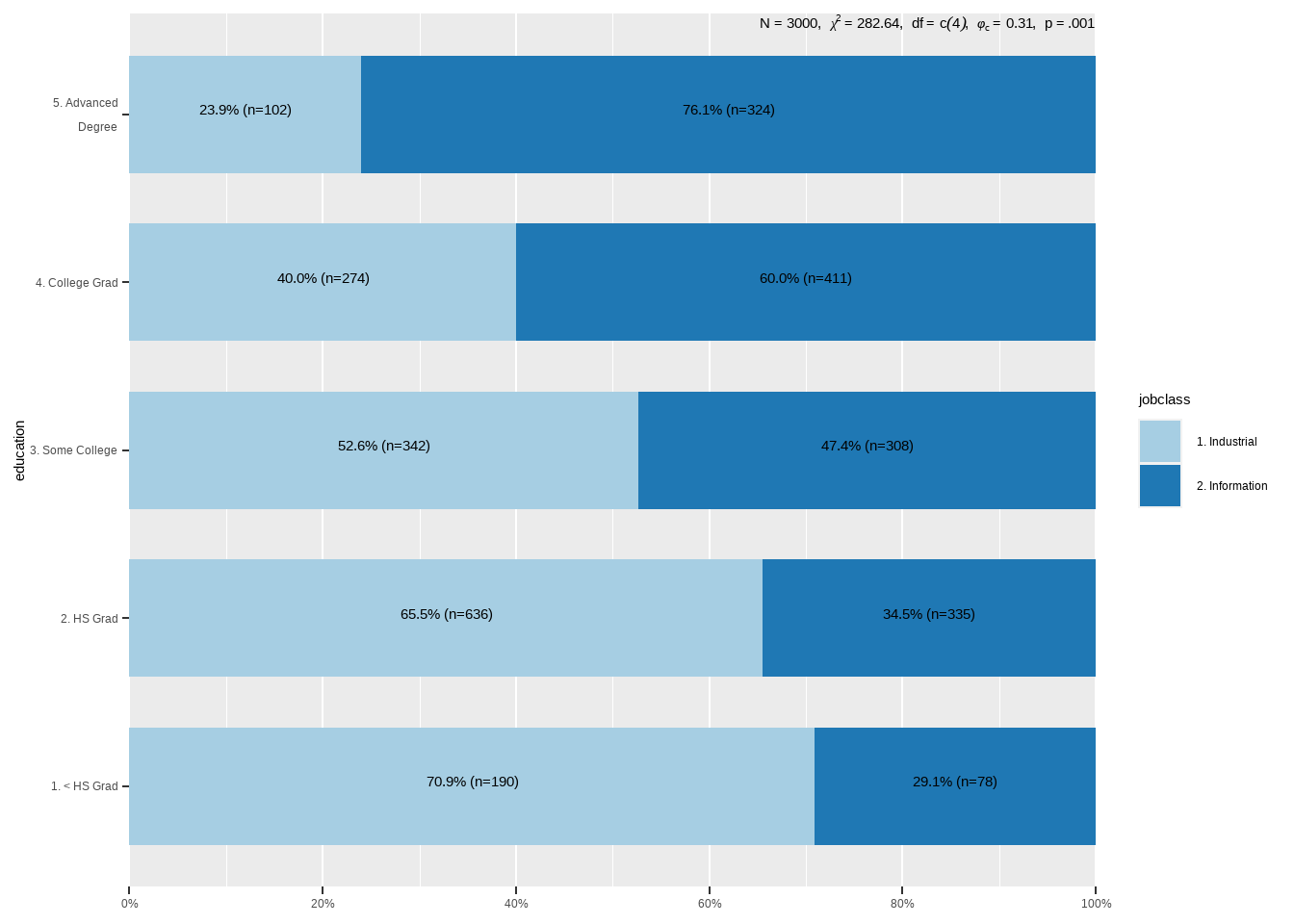
  plot_grid()

#save_plot(filename = "myplot", fig = p, png, width = 30, height = 19)
plot_xtab(x = Wage$education, 
          grp = Wage$jobclass,
          margin = "row",
          bar.pos = "stack",
          show.summary = T,
          coord.flip = T)

tab_xtab(var.row = Wage$education, 
         var.col = Wage$jobclass,
         show.row.prc = T)
education jobclass Total
1. Industrial 2. Information
1. < HS Grad 190
70.9 % 		78
29.1 % 		268
100 %
2. HS Grad 636
65.5 % 		335
34.5 % 		971
100 %
3. Some College 342
52.6 % 		308
47.4 % 		650
100 %
4. College Grad 274
40 % 		411
60 % 		685
100 %
5. Advanced Degree 102
23.9 % 		324
76.1 % 		426
100 %
Total 1544
51.5 % 		1456
48.5 % 		3000
100 %
χ2=282.643 · df=4 · Cramer's V=0.307 · p=0.000

Analyses were conducted using the R Statistical language (version 4.3.2; R Core Team, 2023) on Windows 10 x64 (build 19045), using the packages lme4 (version 1.1.35.1; Bates D et al., 2015), Matrix (version 1.6.1.1; Bates D et al., 2023), likert (version 1.3.5; Bryer J, Speerschneider K, 2016), glmulti (version 1.0.8; Calcagno V, 2020), xtable (version 1.8.4; Dahl D et al., 2019), SmartEDA (version 0.3.9; Dayanand Ubrangala et al., 2022), effects (version 4.2.2; Fox J, Weisberg S, 2019), carData (version 3.0.5; Fox J et al., 2022), lubridate (version 1.9.3; Grolemund G, Wickham H, 2011), DiagrammeR (version 1.0.10; Iannone R, 2023), ISLR (version 1.4; James G et al., 2021), lmerTest (version 3.1.3; Kuznetsova A et al., 2017), sjPlot (version 2.8.15; Lüdecke D, 2023), performance (version 0.10.8; Lüdecke D et al., 2021), report (version 0.5.8; Makowski D et al., 2023), e1071 (version 1.7.14; Meyer D et al., 2023), leaps (version 3.1; Miller TLboFcbA, 2020), tibble (version 3.2.1; Müller K, Wickham H, 2023), dlookr (version 0.6.3; Ryu C, 2024), gtsummary (version 1.7.2; Sjoberg D et al., 2021), rJava (version 1.0.11; Urbanek S, 2024), ggplot2 (version 3.4.4; Wickham H, 2016), forcats (version 1.0.0; Wickham H, 2023), stringr (version 1.5.1; Wickham H, 2023), tidyverse (version 2.0.0; Wickham H et al., 2019), dplyr (version 1.1.4; Wickham H et al., 2023), purrr (version 1.0.2; Wickham H, Henry L, 2023), readr (version 2.1.5; Wickham H et al., 2024) and tidyr (version 1.3.1; Wickham H et al., 2024).

References